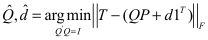Cooperate with Research Scientist Eleni Gourgou and Master Zongyu Li

Significant information is hidden in worms’ locomotion features, as they traverse in Trapezoidal mazes (T-mazes Fig.A) . To understand how the presence of reward (food) on one end of the maze or how learning affects their behavior, our goal of the research is to find the motion trails of C. elegans. The following critical problems: 1) the camera refocusing causing unpredictable shaking; 2) unpredictable noise such as the appearance of bubbles causing tracking the wrong target. After watching hundreds of worm-motion videos and analyzing the common characteristics of them, I found: 1) the duration of the camera refocusing is short; 2) the unpredictable noise only happens outside of T-maze. To solve the first problem, I found the frames in which the shaking happened and discarded them. Then, I used the interpolation method to predict the motion trails of worms in the discarded frames. In this way, we got stable motion trails. To solve the second problem, first, I used the Chan-Vecse active contour method and SVD to extract contours of T-maze (Fig.B red line). Then, I creatively used the matrix approximation method (the Procrustes Transformation method) to only focus on the pixels inside the T-maze and neglect the pixels outside the T-maze (Fig.C), which can be written as.

where T denotes the contour of T-maze, P denotes the T-shape polygon, Q is an unknown unitary rotating matrix and d is an unknown displacement vector.

In this way, even if the unpredictable noise still exists outside the T-maze, it cannot influence the pixels which we really focused on. After that, I applied the Frame Difference method, and we can always track the correct targets (worms) instead of the bubbles. Finally, because the subtle sutbal noise inside T-maze also disturbed the motion trails, so I used the K-Nearest Neighbor (KNN) algorithm to smooth the motion trails (Fig.D, red line: the final trail, green line: trails using the Frame Difference method directly). Cooperating with Zongyu, we coded programs in Matlab for more than 1000 lines to successfully achieve our method.

Publication (submitted):

• Sakelaris B., Li Z., Sun J., Banerjee S., Booth V., Gourgou E.: “Modelling learning in C. elegans chemosensory and locomotive circuitry for T-maze navigation”. (co-second author)
  

MATLAB Code: Github

Video Presentation: YouTube

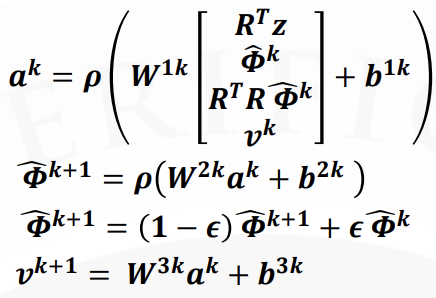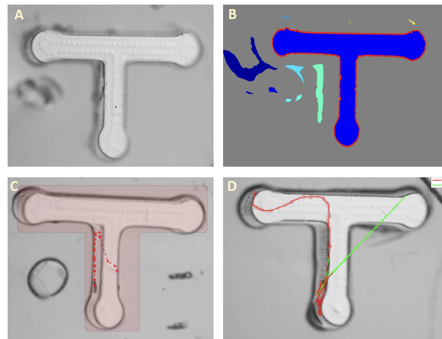
Cooperate with Ph.D Haonan Zhu, Prof Alfred Hero

Our goal of the research is to proposed the left architecture that mimics project gradient descent method from optimization theory.

where k=1,2,...,L denotes the layer number (analogous to number of iteration of projected gradient descent), ρ is the standard ReLU nonlinearity and Φ ^ k is the output at layer k.

I completed the Recurrent Neural Network code with the help of Haonan and under the supervision of Prof Hero.

Advisor: Prof Jie Chen, Prof Lijun Zhang

The beampatterns of circular Differential Microphone Arrays (CDMA) and linear Differential Microphone Arrays (LDMA) are polynomial of sinusoidal function. Classical method of designing beampattern is solving simultaneous equations formed from constrains on the nulls. I prove that the polynomial of sinusoidal function is the solution of a differential equation and the differential equation corresponding to LDMA and CDMA are same. When changing the initial values of the differential equation properly, the solution of the differential equation can be beampatterns of LDMA or beampatterns of CDMA. Therefore, one differential equation can represent two kinds of geometry arrays.

Report of the provement: Github

PPT of the short summary: Github

Advisor: Prof Jie Chen

Distributed PCA method can be obtained by simply approximating the global correlation matrix via the Average Consensus (AC) Algorithm, so matrices are divided in columns. Eigenvalue decomposition of correlation matrix and reduce its dimension to p-dim by PDMM algorithm.

Programming in Matlab to accomplish Distributed PCA.

PPT of the short summary: Github